Advertisements
Advertisements
प्रश्न
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
उत्तर
Given: A ΔABC in which ∠B = ∠C.
DL is the perpendicular from D to AB
DM is the perpendicular from D to AC
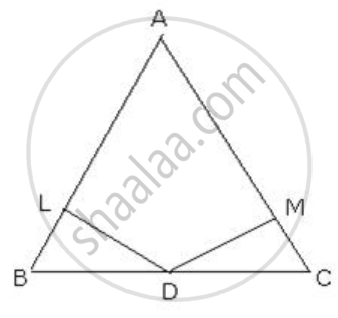
We need to prove that
DL = DM
Proof:
In ΔDLB and ΔDMC
∠DLB = ∠DMC=900 ...[ DL ⊥ AB and DM ⊥ AC ]
∠B=∠C ...[ Given ]
BD= DC ...[ D is the midpoint of BC ]
∴ By Angel-Angel-SIde Criterion of congruence,
ΔDLB ≅ ΔDMC
The corresponding parts of the congruent triangles are congruent.
∴DL=DM ...[ c.p.c.t ]
APPEARS IN
संबंधित प्रश्न
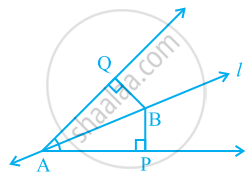
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which congruence criterion do you use in the following?
Given: EB = DB
AE = BC
∠A = ∠C = 90°
So, ΔABE ≅ ΔCDB

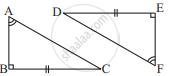
Explain, why ΔABC ≅ ΔFED.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that:
(i) ΔDCE ≅ ΔLBE
(ii) AB = BL.
(iii) AL = 2DC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
