Advertisements
Advertisements
प्रश्न
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
उत्तर
Given: A ΔABC in which ∠B = ∠C.
BP is perpendicular from D to AC
CQ is the perpendicular from C to AB
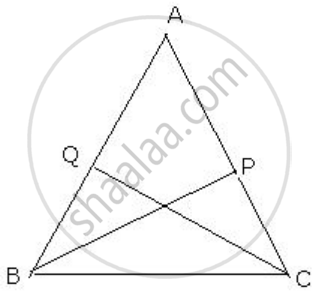
We need to prove that
BP = CQ
Proof:
In ΔBPC and ΔCQB
∠B = ∠C ...[Given]
∠BPC = ∠CQB = 90 ...[BP AC and CQ AB]
BC = BC ...[Common]
∴ BY Angel-Angel-Side criterion of congruence,
ΔBPC ≅ ΔCQB
The corresponding parts of the congruent triangles are congruent.
BP = CQ ...[c.p.c.t]
APPEARS IN
संबंधित प्रश्न
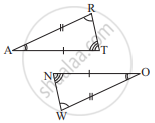
In the figure, the two triangles are congruent.
The corresponding parts are marked. We can write ΔRAT ≅ ?
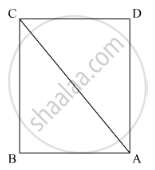
ABCD is a square, X and Yare points on sides AD and BC respectively such that AY = BX. Prove that BY = AX and ∠BAY = ∠ABX.
In the given figure, prove that:
CD + DA + AB > BC
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that: BD = CD

In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
