Advertisements
Advertisements
प्रश्न
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
उत्तर
From M, draw ML such that ML is perpendicular to AB and MN is perpendicular to AC
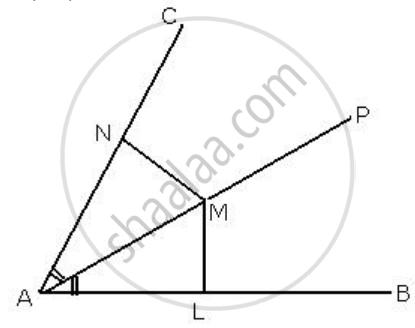
In ΔALM and ΔANM
∠LAM = ∠MAN ...[∵ AP is the bisector of BAC]
∠ALM = ∠ANM = 90° ...[∵ ML ⊥ AB, MN ⊥ AC]
AM = AM ...[Common]
∴ By angle-angle-Side criterion of congruence,
ΔALM ≅ ΔANM
The corresponding parts of the congruent triangles are congruent.
∴ ML = MN ...[c. p. c. t]
Hence, proved.
APPEARS IN
संबंधित प्रश्न
In ΔABC, ∠A = 30°, ∠B = 40° and ∠C = 110°
In ΔPQR, ∠P = 30°, ∠Q = 40° and ∠R = 110°
A student says that ΔABC ≅ ΔPQR by AAA congruence criterion. Is he justified? Why or why not?
If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
