Advertisements
Advertisements
प्रश्न
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
उत्तर
Given: In the figure, O is the center of the circle, and AB is a chord. P is a point on AB such that AP=PB.
We need to prove that, AAP=BP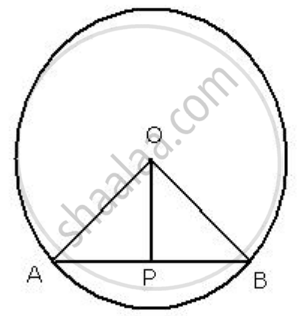
Construction: Join OA and OB
Proof:
In right triangles ΔOAP and ΔOBP
Hypotenuse OA=OB .....[ radii of the same circle ]
Side OP= OP ...[ common ]
∴ By Right Angle- Hypotenuse- Side criterion of congruency, ΔOAP ≅ ΔOBP
The corresponding parts of the congruent triangles are congruent.
∴ AP=BP .....[ by c.p.c.t ]
Hence proved.
APPEARS IN
संबंधित प्रश्न
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

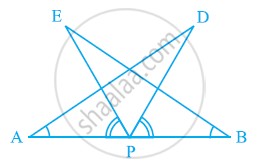
AB is a line segment and P is its mid-point. D and E are points on the same side of AB such that ∠BAD = ∠ABE and ∠EPA = ∠DPB (See the given figure). Show that
- ΔDAP ≅ ΔEBP
- AD = BE
In right triangle ABC, right angled at C, M is the mid-point of hypotenuse AB. C is joined to M and produced to a point D such that DM = CM. Point D is joined to point B (see the given figure). Show that:
- ΔAMC ≅ ΔBMD
- ∠DBC is a right angle.
- ΔDBC ≅ ΔACB
- CM = `1/2` AB

In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

Use the information in the given figure to prove:
- AB = FE
- BD = CF

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
