Advertisements
Advertisements
प्रश्न
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
उत्तर
Given: A ΔABC in which D is the mid-point of BC
AD is produced to E so that DE=AD
We need to prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
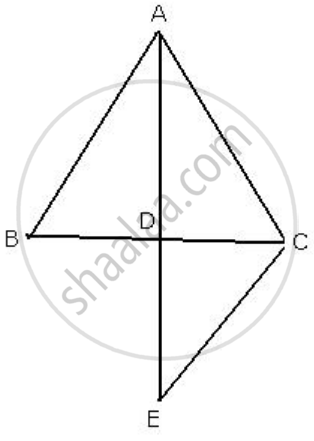
(i) In ΔABD and ΔECD
BD = DC ...[ D is the midpoint of BC ]
∠ADB =∠CDE ...[ vertically opposite angles ]
AD = DE ...[ Given ]
∴ By Side-Angle-Side criterion of congruence, we have,
ΔABD ≅ ΔECD
(ii) The corresponding parts of the congruent triangles are congruent.
∴ AB = EC ...[ c.p.c.t .c]
(iii) Also, ∠BAD = ∠DEC ....[ c.p.c t.c ]
∠ABD = ∠DCE .....[ c.p.c t.c ]
AB || EC .....[ DAB and DEC are alternate angles ]
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
A line segment AB is bisected at point P and through point P another line segment PQ, which is perpendicular to AB, is drawn. Show that: QA = QB.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that: BD = CD

In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
