Advertisements
Advertisements
प्रश्न
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
उत्तर
It is given that ∠A = ∠D , ∠B = ∠E , ∠C = ∠F
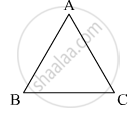
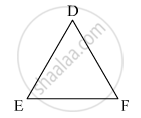
For necessarily triangle to be congruent, sides should also be equal.
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.

In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
In the given figure, prove that:
CD + DA + AB > BC
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
