Advertisements
Advertisements
प्रश्न
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
उत्तर
It is given that ∠A = ∠D , ∠B = ∠E , ∠C = ∠F
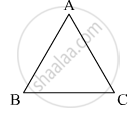
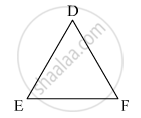
For necessarily triangle to be congruent, sides should also be equal.
APPEARS IN
संबंधित प्रश्न
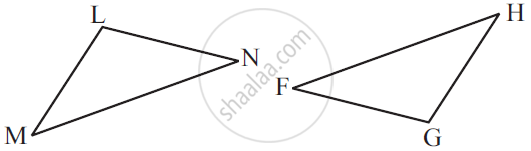
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

You want to show that ΔART ≅ ΔPEN,
If it is given that ∠T = ∠N and you are to use SAS criterion, you need to have
1) RT = and
2) PN =

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

Use the information in the given figure to prove:
- AB = FE
- BD = CF

In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
