Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
उत्तर
Given: ABC is an isosceles triangle with AB = AC and BD and CE are its two medians.
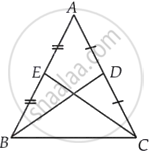
To prove: BD = CE
Proof: In triangle ABC,
AB = AC ...[Given]
`1/2 AB = 1/2 AC`
AE = AD ...[D is the mid-point of AC and E is the mid-point of AB]
Now, in triangle ABD and triangle ACE,
AB = AC ...[Given]
∠A = ∠A ...[Common angle]
AE = AD ...[Above proved]
Now, by SAS criterion of congruence, we get
ΔABD ≅ ΔACE
BD = CE ...[CPCT]
Hence proved.
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
