Advertisements
Advertisements
प्रश्न
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
उत्तर
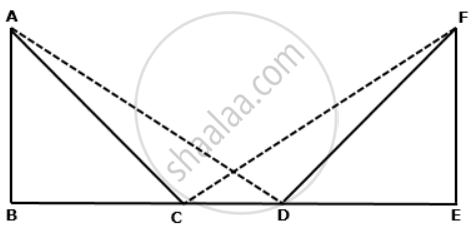Given that, BC = DE
⇒ BC + CD = DE + CD ....( Adding CD on both sides )
⇒ BD = CE ....(i)
Now, in ΔABD and ΔFEC,
AB = EF ....(given)
∠ABD = ∠FEC ....(Each 90°)
BD = CE ....[ From (i) ]
⇒ ΔABD ≅ ΔFEC ...(by SAS congruence criterion)
⇒ AD = FC ...(c.p.c.t.)
APPEARS IN
संबंधित प्रश्न
AD and BC are equal perpendiculars to a line segment AB (See the given figure). Show that CD bisects AB.
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
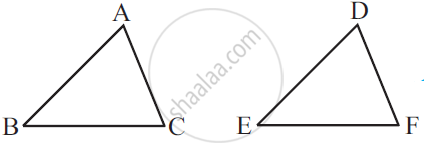
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, AB = PQ, AC = PR, and BC = QR.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
