Advertisements
Advertisements
प्रश्न
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

विकल्प
52°
76°
156°
104°
उत्तर
We are given that;
ΔABC , is isosceles
AB = AC
∠B = ∠C
∠C = 52
And AB || CD
We are asked to find angle x
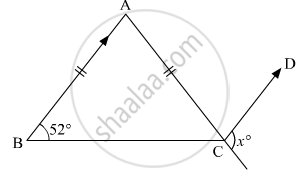
From the figure we have
∠ACB = 52°
Therefore,
∠A = `180° - 2 xx 52° `
= 76°
Since AB || DC , so
∠ACD = ∠BAC
= 76°
Now
x + 76 = 180
= 180 - 76
= 104
APPEARS IN
संबंधित प्रश्न
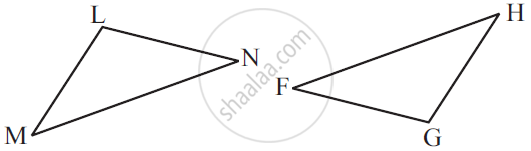
Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In quadrilateral ABCD, AD = BC and BD = CA.
Prove that:
(i) ∠ADB = ∠BCA
(ii) ∠DAB = ∠CBA
A point O is taken inside a rhombus ABCD such that its distance from the vertices B and D are equal. Show that AOC is a straight line.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
