Advertisements
Advertisements
प्रश्न
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
उत्तर
Given: A(Δ ABC) is right-angled at B.
ABPQ and ACRS are squares
To Prove:
(i) ΔACQ ≅ ΔASB
(ii) CQ = BS
Proof:
(i)
∠ QAB = 90° ...[ ABPQ is a square ] ...(1)
∠ CAS = 90° ...[ ACRS is a square ] ...(2)
From (1) and (2) , We have
∠ QAB = ∠CAS ...(3)
Adding ∠BAC to both sides of (3), We have
∠ QAB + ∠BAC = ∠CAS+ ∠BAC
⇒ ∠QAC = ∠BAS ...(4)
In ΔACQ ≅ ΔASB, (by SAS)
QA = AB ...[ Sides of a square ABPQ ]
∠QAC = ∠SAB ...[ From(4) ]
AC = AS ...[ sides of a square ACRS ]
∴ By Side -Angle-Side criterion of congruence,
ΔACQ ≅ ΔASB
(ii)
The corresponding parts of the congruent triangles are congruent,
∴ CQ = SB ...[ c.p.c.t. ]
APPEARS IN
संबंधित प्रश्न
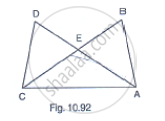
In Fig. 10.92, it is given that AB = CD and AD = BC. Prove that ΔADC ≅ ΔCBA.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
The given figure shows a circle with center O. P is mid-point of chord AB.

Show that OP is perpendicular to AB.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the given figure: AB//FD, AC//GE and BD = CE;
prove that:
- BG = DF
- CF = EG

In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD ≅ ΔBPC
(ii) Find the angles of ΔDPC.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
In a triangle, ABC, AB = BC, AD is perpendicular to side BC and CE is perpendicular to side AB.
Prove that: AD = CE.
