Advertisements
Advertisements
प्रश्न
In a ΔABC, BD is the median to the side AC, BD is produced to E such that BD = DE.
Prove that: AE is parallel to BC.
उत्तर
Given: A(ΔABC) in which BD is the median to AC.
BD is produced to E such that BD = DE,
We need to prove that AE II BC.
Construction: Join AE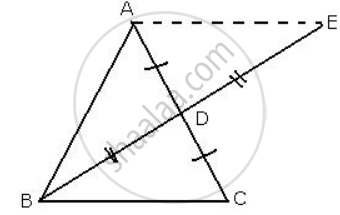
Proof:
AD = DC ...[ BD is median to AC ] ...(1)
In ΔBDC and ΔADE,
BD = DE ...[ Given ]
∠BDC = ∠ADE = 90° ...[ Vertically opposite angles ]
AD = DC ...[ from(1) ]
∴ By Side-Angle-Side Criterion of congruence,
ΔBDC ≅ ΔADE
The corresponding parts of the congruent triangles are congruent.
∴ ∠EAD = ∠BCD ...[ c.p.c.t. ]
But these are alternate angles and AC is the transversal.
Thus, AE || BC.
APPEARS IN
संबंधित प्रश्न
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
You want to show that ΔART ≅ ΔPEN,
If you have to use SSS criterion, then you need to show
1) AR =
2) RT =
3) AT =

You have to show that ΔAMP ≅ AMQ.
In the following proof, supply the missing reasons.
| Steps | Reasons | ||
| 1 | PM = QM | 1 | ... |
| 2 | ∠PMA = ∠QMA | 2 | ... |
| 3 | AM = AM | 3 | ... |
| 4 | ΔAMP ≅ ΔAMQ | 4 | ... |

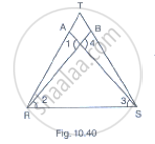
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
If ABC and DEF are two triangles such that AC = 2.5 cm, BC = 5 cm, ∠C = 75°, DE = 2.5 cm, DF = 5cm and ∠D = 75°. Are two triangles congruent?
In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
AD and BC are equal perpendiculars to a line segment AB. If AD and BC are on different sides of AB prove that CD bisects AB.
