Advertisements
Advertisements
प्रश्न
In two congruent triangles ABC and DEF, if AB = DE and BC = EF. Name the pairs of equal angles.
उत्तर
It is given that
ΔABC ≅ ΔDEF
AB = DE
BC = EF
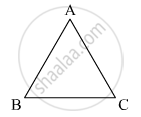
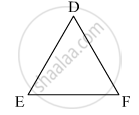
Since, the triangles ABC and DEF are congruent, therefore,
∠A = ∠D
∠B = ∠E
∠C = ∠F
APPEARS IN
संबंधित प्रश्न
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
D, E, F are the mid-point of the sides BC, CA and AB respectively of ΔABC. Then ΔDEF is congruent to triangle
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
prove that : AL = 2DC
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
