Advertisements
Advertisements
प्रश्न
ABC is an isosceles triangle in which AB = AC. BE and CF are its two medians. Show that BE = CF.
उत्तर
In the triangle ABC it is given that
AB = AC, BE and CFare medians.
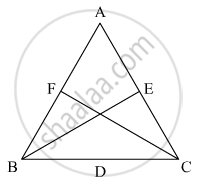
We have to show that BE CF
To show BF = CF we will show that ΔBFC ≅ ΔBEC
In triangle ΔBFC and ΔBEC
As AB = AC, so
∠FBC = ∠ECF .........(1)
BC=BC (common sides) ........(2)
Since,
AB = AC
`1/2 AB =1/2 AC `
As F and E are mid points of sides AB and AC respectively, so
BF = CE ..........(3)
From equation (1), (2), and (3)
ΔBFC and ΔBEC
Hence FC = BE Proved.
APPEARS IN
संबंधित प्रश्न
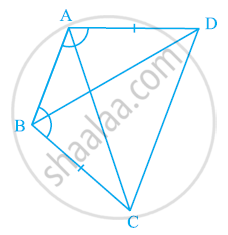
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
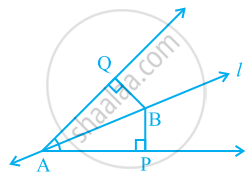
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
In the given figure, ABC is an isosceles triangle whose side AC is produced to E. Through C, CD is drawn parallel to BA. The value of x is

A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
ABCD is a parallelogram. The sides AB and AD are produced to E and F respectively, such produced to E and F respectively, such that AB = BE and AD = DF.
Prove that: ΔBEC ≅ ΔDCF.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
