Advertisements
Advertisements
प्रश्न
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
उत्तर
It is given that
∠B = 35°
∠C = 65°
AP is the bisector of ∠CAB
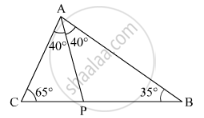
We have to arrangeAP, BPand CPin descending order.
In ΔACP we have
∠ACP = 65°
∠CAP = 40°(As AP is the bisector of ∠CAB
So AP > CP (Sides in front or greater angle will be greater) ........(1)
In ΔABP we have
∠BAP = 40°(As AP is the bisector of ∠CAB)
Since,
∠BAP >∠ABP
So BP > AP ..........(2)
Hence
From (1) & (2) we have
BP > AP > CP
APPEARS IN
संबंधित प्रश्न
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

In the given figure, prove that:
CD + DA + AB > BC
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
The following figure shows a circle with center O.

If OP is perpendicular to AB, prove that AP = BP.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In the figure, given below, triangle ABC is right-angled at B. ABPQ and ACRS are squares. 
Prove that:
(i) ΔACQ and ΔASB are congruent.
(ii) CQ = BS.
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.
Prove that : (i) BO = CO
(ii) AO bisects angle BAC.
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
Which of the following is not a criterion for congruence of triangles?
