Advertisements
Advertisements
Question
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
Advertisements
Solution
It is given that
∠B = 35°
∠C = 65°
AP is the bisector of ∠CAB
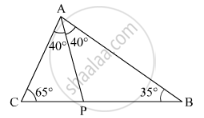
We have to arrangeAP, BPand CPin descending order.
In ΔACP we have
∠ACP = 65°
∠CAP = 40°(As AP is the bisector of ∠CAB
So AP > CP (Sides in front or greater angle will be greater) ........(1)
In ΔABP we have
∠BAP = 40°(As AP is the bisector of ∠CAB)
Since,
∠BAP >∠ABP
So BP > AP ..........(2)
Hence
From (1) & (2) we have
BP > AP > CP
APPEARS IN
RELATED QUESTIONS
In the given figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Show that BC = DE.
Which congruence criterion do you use in the following?
Given: AC = DF
AB = DE
BC = EF
So, ΔABC ≅ ΔDEF
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from B and C to the opposite sides are equal.
From the given diagram, in which ABCD is a parallelogram, ABL is a line segment and E is mid-point of BC.
Prove that: AB = BL.
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
In the following diagram, ABCD is a square and APB is an equilateral triangle.
- Prove that: ΔAPD ≅ ΔBPC
- Find the angles of ΔDPC.
In the following figure, AB = EF, BC = DE and ∠B = ∠E = 90°.
Prove that AD = FC.
