Advertisements
Advertisements
Question
In quadrilateral ACBD, AC = AD and AB bisects ∠A (See the given figure). Show that ΔABC ≅ ΔABD. What can you say about BC and BD?

Solution
Given: In quadrilateral ABCD, AC = AD and AB bisects ∠A.
To prove: △ABC ≌ △ABD
Proof: In △ABC and △ABD,
AC = AD ...[Given]
∠BAC = ∠BAD ...[∵ AB bisects ∠A]
AB = AB ...[Common]
∴ △ABC ≌ △ABD ...[By SAS congruence rule]
Hence, BC = BD ...[Corresponding parts of congruent triangles]
APPEARS IN
RELATED QUESTIONS
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

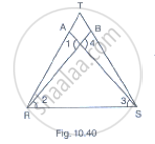
In Fig. 10.40, it is given that RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
The perpendicular bisectors of the sides of a triangle ABC meet at I.
Prove that: IA = IB = IC.
In ∆ABC, AB = AC. Show that the altitude AD is median also.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the adjoining figure, QX and RX are the bisectors of the angles Q and R respectively of the triangle PQR.
If XS ⊥ QR and XT ⊥ PQ ;
prove that: (i) ΔXTQ ≅ ΔXSQ.
(ii) PX bisects angle P.
In the following figure, OA = OC and AB = BC.
Prove that: ΔAOD≅ ΔCOD
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
ABC is an isosceles triangle with AB = AC and BD and CE are its two medians. Show that BD = CE.
