Advertisements
Advertisements
Question
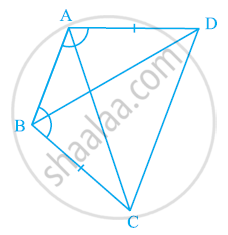
ABCD is a quadrilateral in which AD = BC and ∠DAB = ∠CBA (See the given figure). Prove that
- ΔABD ≅ ΔBAC
- BD = AC
- ∠ABD = ∠BAC.
Solution
In quadrilateral ABCD, we have
AD = BC and ∠DAB = ∠CBA
i. In ΔABD and ΔBAC,
AD = BC ...[Given]
∠DAB = ∠CBA ...[Given]
AB = BA ...[Common]
∴ ΔABD ≅ ΔBAC ...[By SAS congruency]
ii. Since ΔABD ≅ ΔBAC
BD = AC ...[By Corresponding parts of congruent triangles]
iii. Since ΔABD ≅ ΔBAC
∠ABD = ∠BAC ...[By Corresponding parts of congruent triangles]
APPEARS IN
RELATED QUESTIONS
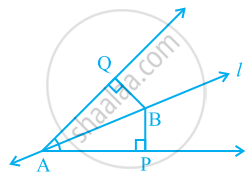
Line l is the bisector of an angle ∠A and B is any point on l. BP and BQ are perpendiculars from B to the arms of ∠A (see the given figure). Show that:
- ΔAPB ≅ ΔAQB
- BP = BQ or B is equidistant from the arms of ∠A.
Which of the following statements are true (T) and which are false (F):
Two right triangles are congruent if hypotenuse and a side of one triangle are respectively equal equal to the hypotenuse and a side of the other triangle.
Prove that the perimeter of a triangle is greater than the sum of its altitudes.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
A triangle ABC has ∠B = ∠C.
Prove that: The perpendiculars from the mid-point of BC to AB and AC are equal.
In the following figure, BL = CM.

Prove that AD is a median of triangle ABC.
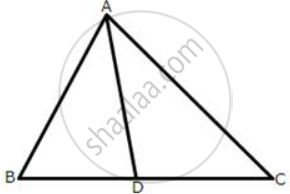
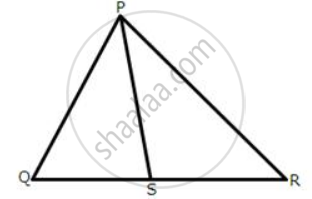
In the following figures, the sides AB and BC and the median AD of triangle ABC are equal to the sides PQ and QR and median PS of the triangle PQR.
Prove that ΔABC and ΔPQR are congruent.
 |
 |
PQRS is a parallelogram. L and M are points on PQ and SR respectively such that PL = MR.
Show that LM and QS bisect each other.
