Advertisements
Advertisements
Question
In triangles ABC and CDE, if AC = CE, BC = CD, ∠A = 60°, ∠C = 30° and ∠D = 90°. Are two triangles congruent?
Solution
For the triangles ABC and ECD, we have the following information and corresponding figure:
AC = CE
BC = CD
∠A = 60°
∠C = 30°
∠D = 90°
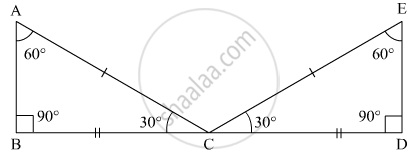
In triangles ABC and ECD, we have
AC = EC
BC = CD
and ∠BAC= ∠CED
The SSA criteria for two triangles to be congruent are being followed. So both the triangles are congruent.
APPEARS IN
RELATED QUESTIONS
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.

Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ

Which congruence criterion do you use in the following?
Given: ∠MLN = ∠FGH
∠NML = ∠GFH
ML = FG
So, ΔLMN ≅ ΔGFH
You want to show that ΔART ≅ ΔPEN,
If it is given that AT = PN and you are to use ASA criterion, you need to have
1) ?
2) ?

If perpendiculars from any point within an angle on its arms are congruent, prove that it lies on the bisector of that angle.
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.

In the given figure, prove that:
CD + DA + AB + BC > 2AC

In two triangles ABC and ADC, if AB = AD and BC = CD. Are they congruent?
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB is parallel to EC.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
