Advertisements
Advertisements
Question
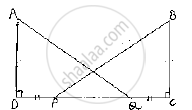
In Fig. 10.99, AD ⊥ CD and CB ⊥. CD. If AQ = BP and DP = CQ, prove that ∠DAQ = ∠CBP.
Advertisements
Solution
Given that, in the figure AD ⊥ CD and CB ⊥ CD and AQ = BP,DP =CQ
We have to prove that ∠DAQ=∠CBP
Given that DP= QC
Add PQ on both sides
Given that DP=QC
Add PQ on both sides
⇒ DP+PQ=PQ+QC
⇒ DQ=PC ................(1)
Now, consider triangle DAQ and CBP,
We have
∠ADQ=∠BCP=90° [given]
AQ=BP [given]
And DQ=PC [given]
So, by RHS congruence criterion, we have ΔDAQ≅ΔCBP
Now,
∠DAQ=∠CBP [ ∵Corresponding parts of congruent triangles are equal]
∴ Hence proved
APPEARS IN
RELATED QUESTIONS
l and m are two parallel lines intersected by another pair of parallel lines p and q (see the given figure). Show that ΔABC ≅ ΔCDA.
Which congruence criterion do you use in the following?
Given: ZX = RP
RQ = ZY
∠PRQ = ∠XZY
So, ΔPQR ≅ ΔXYZ
If ΔABC and ΔPQR are to be congruent, name one additional pair of corresponding parts. What criterion did you use?
In Δ ABC, ∠B = 35°, ∠C = 65° and the bisector of ∠BAC meets BC in P. Arrange AP, BP and CP in descending order.
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
The given figure shows a circle with center O. P is mid-point of chord AB.
Show that OP is perpendicular to AB.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD. Prove that:
AB = CE.
In the following diagram, AP and BQ are equal and parallel to each other. 
Prove that: AB and PQ bisect each other.
In the following figure, ∠A = ∠C and AB = BC.
Prove that ΔABD ≅ ΔCBE. 
In the following figure, ABC is an equilateral triangle in which QP is parallel to AC. Side AC is produced up to point R so that CR = BP.
Prove that QR bisects PC.
Hint: ( Show that ∆ QBP is equilateral
⇒ BP = PQ, but BP = CR
⇒ PQ = CR ⇒ ∆ QPM ≅ ∆ RCM ).
