Advertisements
Advertisements
Question
Which of the following statements are true (T) and which are false (F):
Sides opposite to equal angles of a triangle may be unequal
Solution
False (F)
Reason: Sides opposite to equal angles of a triangle are equal
APPEARS IN
RELATED QUESTIONS
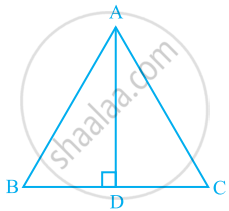
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
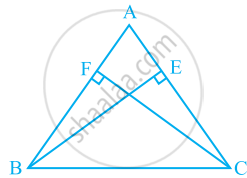
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
Show that the angles of an equilateral triangle are 60° each.
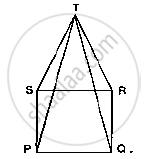
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
In a ΔABC, if ∠A=l20° and AB = AC. Find ∠B and ∠C.
Which of the following statements are true (T) and which are false (F):
Angles opposite to equal sides of a triangle are equal
Fill the blank in the following so that the following statement is true.
In an equilateral triangle all angles are .....
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
In a ΔABC, ∠A = 50° and BC is produced to a point D. If the bisectors of ∠ABC and ∠ACDmeet at E, then ∠E =
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
