Advertisements
Advertisements
Question
In Fig. 10.23, PQRS is a square and SRT is an equilateral triangle. Prove that
(i) PT = QT (ii) ∠TQR = 15°
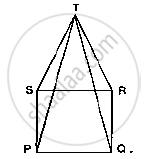
Solution
Given that PQRS is a square and SRT is an equilateral triangle. And given to prove that

PT = QT and ∠ TQR =15 °
Now , PQRS is a square
⇒ PQ =QR=RS=SP ....................... (1)
And also, SRT is an equilateral triangle.
⇒ SR = RT=TS .............................(2)
And ∠TSR = ∠SRT= ∠RTS = 60°
From (1) and (2)
PQ=QR=SP=SR=RT=TS ...........................(3)
And also,
∠TSR=∠TSR+∠RSP= 60° +90° +150°
∠TRQ=∠TRS+∠SRQ=60°+90°+150°
⇒ ∠TSR=∠TRQ=150° ............................(4)
Now, in Δ TSR and Δ TRQ
TS=TR [from (3)]Δ
∠TSP = ∠TRQ [from (4)]
SP=RQ [from (3)]
So, by SAS ccongruence criterion we have
Δ TSR ≅ Δ TRQ
⇒ PT=QT [corresponding parts of congruent triangles are equal ]
Consider Δ TQR,
QR= TR [from (3)]
⇒ Δ TQR is a isosceles triangle
∠QTR=∠TQR [angles opposite to equal sides]
Now,
Sum of angles in a traingle is qual to 180°
⇒ ∠ QTR+∠TQR + ∠TRQ =180°
⇒ 2∠TQR+150°=180 [from (4)]
⇒ 2∠TQR = 180° -150°
⇒ 2 ∠TQR = 30° ∠TQR=15 °
∴ Hence Proved
APPEARS IN
RELATED QUESTIONS
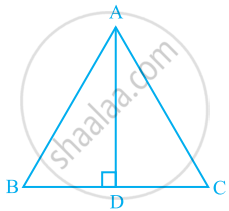
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
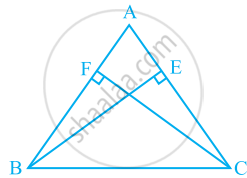
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
Find the measure of each exterior angle of an equilateral triangle.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
Fill the blank in the following so that the following statement is true.
In right triangles ABC and DEF, if hypotenuse AB = EF and side AC = DE, then ΔABC ≅ Δ ……
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
In a triangle ABC, if AB = AC and AB is produced to D such that BD = BC, find ∠ACD: ∠ADC.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
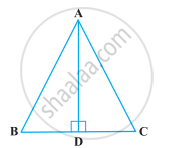
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
