Advertisements
Advertisements
Question
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
Solution
No. Here, we see that 9 + 7 = 16 < 17
i.e., the sum of two sides of a triangle is less than the third side.
Hence, it contradicts the property that the sum of two sides of a triangle is greater than the third side.
Therefore, it is not possible to construct a triangle with given sides.
APPEARS IN
RELATED QUESTIONS
The vertical angle of an isosceles triangle is 100°. Find its base angles.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.
ABC is a triangle and D is the mid-point of BC. The perpendiculars from D to AB and AC are equal. Prove that the triangle is isosceles.
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
Fill in the blank to make the following statement true.
In a right triangle the hypotenuse is the .... side.
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
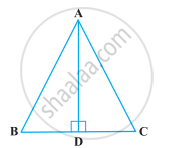
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
Show that in a quadrilateral ABCD, AB + BC + CD + DA < 2(BD + AC)
