Question

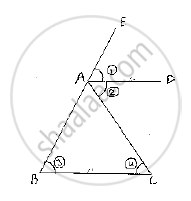
If the bisector of the exterior vertical angle of a triangle be parallel to the base. Show that the triangle is isosceles.  

Answer 1

Given that the bisector of the exterior vertical angle of a triangle is parallel to the base and we have to prove that the triangle is isosceles Let ABC be a triangle such that AD is the angular bisector of exterior vertical angle EAC and AD|| BC   

Let ∠EAD= (1),∠DAC = (2),∠ABC = (3) and ∠ACB =(4) 

We have, 

(1) = (2)             [ ∵AD is bisector of EAC ]  

(1) = (3)            [Corresponding angles] 

and (2) = (4)          [alternative angle] 

⇒(3)=(4)⇒AB=AC 

Since, in ΔABC, two sides AB and AC are equal we can say that  ΔABC is isosceles