Topics
Number Systems
Number Systems
Polynomials
Algebra
Coordinate Geometry
Linear Equations in Two Variables
Geometry
Coordinate Geometry
Introduction to Euclid’S Geometry
Mensuration
Statistics and Probability
Lines and Angles
- Introduction to Lines and Angles
- Basic Terms and Definitions
- Intersecting Lines and Non-intersecting Lines
- Introduction to Parallel Lines
- Pairs of Angles
- Parallel Lines and a Transversal
- Angle Sum Property of a Triangle
Triangles
- Concept of Triangles
- Congruence of Triangles
- Criteria for Congruence of Triangles
- Properties of a Triangle
- Some More Criteria for Congruence of Triangles
- Inequalities in a Triangle
Quadrilaterals
- Concept of Quadrilaterals
- Properties of a Quadrilateral
- Types of Quadrilaterals
- Another Condition for a Quadrilateral to Be a Parallelogram
- Theorem of Midpoints of Two Sides of a Triangle
- Property: The Opposite Sides of a Parallelogram Are of Equal Length.
- Theorem: A Diagonal of a Parallelogram Divides It into Two Congruent Triangles.
- Theorem : If Each Pair of Opposite Sides of a Quadrilateral is Equal, Then It is a Parallelogram.
- Property: The Opposite Angles of a Parallelogram Are of Equal Measure.
- Theorem: If in a Quadrilateral, Each Pair of Opposite Angles is Equal, Then It is a Parallelogram.
- Property: The diagonals of a parallelogram bisect each other. (at the point of their intersection)
- Theorem : If the Diagonals of a Quadrilateral Bisect Each Other, Then It is a Parallelogram
Circles
Areas - Heron’S Formula
Surface Areas and Volumes
Statistics
Algebraic Expressions
Algebraic Identities
Area
Constructions
- Introduction of Constructions
- Basic Constructions
- Some Constructions of Triangles
Probability
Notes
Construct a triangle in which two sides are equal, say each equal to 3.5 cm and the third side equal to 5 cm in following fig. 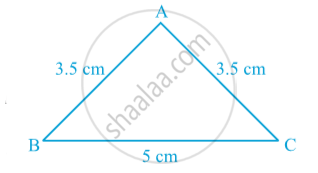
A triangle in which two sides are equal is called an isosceles triangle. So, ∆ ABC of above Fig. is an isosceles triangle with AB = AC.
Theorem
Theorem : Angles opposite to equal sides of an isosceles triangle are equal.
Proof : We are given an isosceles triangle ABC in which AB = AC. We need to prove that ∠ B = ∠ C. Let us draw the bisector of ∠ A and let D be the point of intersection of this bisector of
∠ A and BC in following fig.
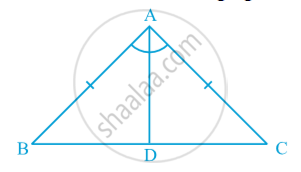
In ∆ BAD and ∆ CAD,
AB = AC (Given)
∠ BAD = ∠ CAD (By construction)
AD = AD (Common)
So, ∆ BAD ≅ ∆ CAD (By SAS rule)
So, ∠ ABD = ∠ ACD, since they are corresponding angles of congruent triangles.
So, ∠ B = ∠ C
Theorem : The sides opposite to equal angles of a triangle are equal.
This is converse of above theorem.