Advertisements
Advertisements
Question
It is given that ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40° and ∠A = 80°. Then which of the following is true?
Options
DF = 5 cm, ∠F = 60°
DF = 5 cm, ∠E = 60°
DE = 5 cm, ∠E = 60°
DE = 5 cm, ∠D = 40°
Solution
DF = 5 cm, ∠E = 60°
Explanation:
Given, ∆ABC ≅ ∆FDE and AB = 5 cm, ∠B = 40°, ∠A = 80°
Since, ∆FDE ≅ ∆ABC
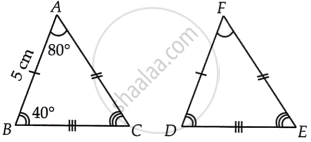
∴ DF = AB ...[By CPCT]
DF = 5 cm
And ∠E = ∠C ...[By CPCT]
⇒ ∠E = ∠C = 180° – (∠A + ∠B) ...[By angle sum property of a ∆ABC]
⇒ ∠E = 180° – (80° + 40°)
⇒ ∠E = 60°
APPEARS IN
RELATED QUESTIONS
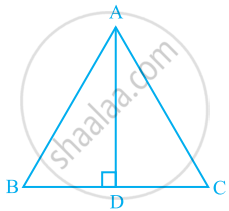
In ΔABC, AD is the perpendicular bisector of BC (see the given figure). Show that ΔABC is an isosceles triangle in which AB = AC.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Prove that the medians of an equilateral triangle are equal.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Prove that each angle of an equilateral triangle is 60°.
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
In ∆PQR, ∠R = ∠P and QR = 4 cm and PR = 5 cm. Then the length of PQ is ______.
