Advertisements
Advertisements
Question
If the measures of angles of a triangle are in the ratio of 3 : 4 : 5, what is the measure of the smallest angle of the triangle?
Options
25°
30°
45°
60°
Solution
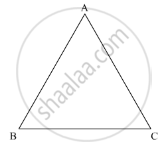
In the given figure, measures of the angles of ΔABC are in the ratio 3 : 4 : 5. We need to find the measure of the smallest angle of the triangle.
Let us take,
∠A = 3x
∠B = 4x
∠C = 5x
Now, applying angle sum property of the triangle in ΔABC, we get,
∠A + ∠B + ∠C = 180°
3x + 4x + 5x = 180°
12X = 180°
`x = (180°)/ 12`
x = 15°
Substituting the value of x in ,∠A,∠Band∠C
∠A = 3(15°) = 45
∠B = 4(15V) = 60
∠C = 5(15°) = 75°
Since, the measure of ∠A is the smallest
Thus, the measure of the smallest angle of the triangle is 45°
APPEARS IN
RELATED QUESTIONS
Find the measure of each exterior angle of an equilateral triangle.
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Which of the following statements are true (T) and which are false (F):
If the bisector of the vertical angle of a triangle bisects the base, then the triangle may be isosceles.
In a ΔABC, if ∠B = ∠C = 45°, which is the longest side?
In ΔABC, if ∠A = 40° and ∠B = 60°. Determine the longest and shortest sides of the triangle.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
Line segments AB and CD intersect at O such that AC || DB. If ∠CAB = 45° and ∠CDB = 55°, then ∠BOD =
In triangles ABC and PQR, AB = AC, ∠C = ∠P and ∠B = ∠Q. The two triangles are ______.
Is it possible to construct a triangle with lengths of its sides as 9 cm, 7 cm and 17 cm? Give reason for your answer.
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.