Advertisements
Advertisements
Question
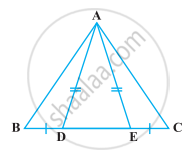
In the following figure, D and E are points on side BC of a ∆ABC such that BD = CE and AD = AE. Show that ∆ABD ≅ ∆ACE.
Solution
Given: D and E are the points on side BC of a ∆ABC such that BD = CE and AD = AE.
To show: ∆ABD ≅ ∆ACE
Proof: We have, AD = AE ...[Given]
⇒ ∠ADE = ∠AED ...(i) [Since, angles opposite to equal sides are equal]
We have, ∠ADB + ∠ADE = 180° ...[Linear pair axiom]
⇒ ∠ADB = 180° – ∠ADE
= 180° – ∠AED ...[From equation (i)]
In ∆ABD and ∆ACE,
∠ADB = ∠AEC ...[∵ ∠AEC + ∠AED = 180°, linear pair axiom]
BD = CE ...[Given]
And AD = AE ...[Given]
∴ ∆ABD ≅ ∆ACE ...[By SAS congruence rule]
APPEARS IN
RELATED QUESTIONS
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
Prove that the medians of an equilateral triangle are equal.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
In the given figure, what is the value of x?
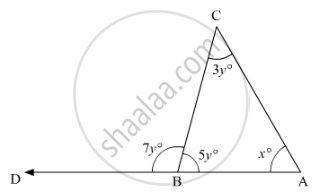
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
In ∆ABC, AB = AC and ∠B = 50°. Then ∠C is equal to ______.
In ∆PQR, if ∠R > ∠Q, then ______.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
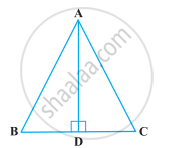
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
