Advertisements
Advertisements
Question
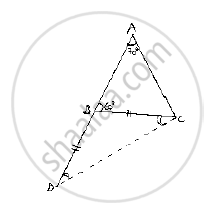
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
Solution
Given that in ΔABC,side AB is produced to D So that BD = BC and ∠B =60°,∠A= 70°
We have to prove that
(1)AD>CD (2)AD>AC
First join C and D
Now, in ΔABC
∠A+∠B+∠C=180° [ ∵ Sum of angles in a triangle 180° ]
⇒ ∠C=180°-70°-60°
=180°-130°=50°
∴ ∠C=50° ⇒ ∠ACB=50° ..............(1)
And also in ,Δ BDC,
∠DBC=180°-∠ABC [∵ABDis a straight angle ]
=180°-60°=120°
and also BD=BC [given]
⇒ ∠BCD=∠BDC [ ∵Angles opposite to equal sides are equal]
Now,
∠DBC+∠BCD+∠BDC=180° [ ∵Sum of angles in a triangle 180°]
⇒ 120°+∠BCD+∠BCD=180°
⇒2∠BCD=180°-120°⇒ ∠BCD=`(60°) /2=30`
∴ ∠BCD=∠BDC=30° ..............(2)
Now, consider , ΔADC,
∠BAC⇒∠DAC=70 [given]
∠BDC⇒∠ADC=30 [ ∵ From (2)]
∠ACD=∠ACB+∠BCD
=50°+ 30° [ ∵ From (1) and (2)]
=80°
Now, ∠ADC<∠DAC<ACD
⇒ AC<DC<AD
[∵ Side opposite to greater angle is longer and smaller angle is smaller]
⇒ AD>DC and AD>AC
∴Hence proved
Or
We have, ∠ACD>∠DAC and ∠ACD>∠ADC
⇒ AD>DC and AD>AC
[ ∵ Side opposite to greater angle is longer and smaller angle is smaller]
APPEARS IN
RELATED QUESTIONS
AB is a line seg P and Q are points on opposite sides of AB such that each of them is equidistant from the points A and B (See Fig. 10.26). Show that the line PQ is perpendicular bisector of AB.
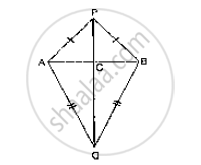
Two lines AB and CD intersect at O such that BC is equal and parallel to AD. Prove that the lines AB and CD bisect at O.
Which of the following statements are true (T) and which are false (F)?
Difference of any two sides of a triangle is equal to the third side.
If the angles of a triangle are in the ratio 2 : 1 : 3, then find the measure of smallest angle.
If the angles A, B and C of ΔABC satisfy the relation B − A = C − B, then find the measure of ∠B.
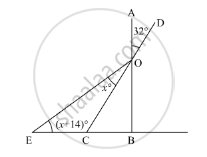
In the given figure, if AB ⊥ BC. then x =
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
Which of the following correctly describes the given triangle?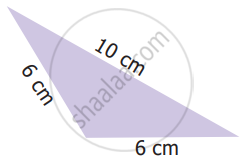
Show that in a quadrilateral ABCD, AB + BC + CD + DA > AC + BD
In a triangle ABC, D is the mid-point of side AC such that BD = `1/2` AC. Show that ∠ABC is a right angle.
