Advertisements
Advertisements
Question
The base BC of triangle ABC is produced both ways and the measure of exterior angles formed are 94° and 126°. Then, ∠BAC =
Options
94°
54°
40°
44°
Advertisements
Solution
the given problem, the exterior angles obtained on producing the base of a triangle both ways are 94°and 126°. So, let us draw ΔABC and extend the base BC, such that:
∠ACD = 126°
∠ABE = 94°
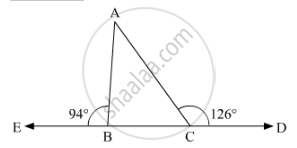
Here, we need to find ∠BAC
Now, since BCD is a straight line, using the property, “angles forming a linear pair are supplementary”, we get
∠ AC+ ∠ ACD = 180°
∠ ACB + 126° = 180°
∠ ACB = 180° - 126°
∠ ACB = 54°
Similarly, EBS is a straight line, so we get,
∠ ABC + ∠ ABE = 180°
∠ ABC + 94° = 180°
∠ ABC = 180° - 94°
∠ ABC = 86°
Further, using angle sum property in ΔABC
∠ ABC + ∠ ACB + ∠ BAC = 180°
54° + 86° + ∠ BAC = 180°
∠ BAC = 180° - 140°
∠ BAC = 40°
Thus, ∠ BAC = 40°
APPEARS IN
RELATED QUESTIONS
Find the measure of each exterior angle of an equilateral triangle.
In figure, AB = AC and DB = DC, find the ratio ∠ABD : ∠ACD
Prove that the medians of an equilateral triangle are equal.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
If the base of an isosceles triangle is produced on both sides, prove that the exterior angles so formed are equal to each other.
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that LN = MN.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
Fill the blank in the following so that the following statement is true.
Angle opposite to equal sides of a triangle are .....
Which of the following statements are true (T) and which are false (F)?
If two angles of a triangle are unequal, then the greater angle has the larger side opposite to it.
Fill in the blank to make the following statement true.
If two sides of a triangle are unequal, then the larger side has .... angle opposite to it.
In the given figure, what is z in terms of x and y?
Two sides of a triangle are of lengths 5 cm and 1.5 cm. The length of the third side of the triangle cannot be ______.
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
AD is a median of the triangle ABC. Is it true that AB + BC + CA > 2AD? Give reason for your answer.
M is a point on side BC of a triangle ABC such that AM is the bisector of ∠BAC. Is it true to say that perimeter of the triangle is greater than 2 AM? Give reason for your answer.
Find all the angles of an equilateral triangle.
ABC is an isosceles triangle with AB = AC and D is a point on BC such that AD ⊥ BC (Figure). To prove that ∠BAD = ∠CAD, a student proceeded as follows:
In ∆ABD and ∆ACD,
AB = AC (Given)
∠B = ∠C (Because AB = AC)
and ∠ADB = ∠ADC
Therefore, ∆ABD ≅ ∆ACD (AAS)
So, ∠BAD = ∠CAD (CPCT)
What is the defect in the above arguments?
[Hint: Recall how ∠B = ∠C is proved when AB = AC].
