Advertisements
Advertisements
Question
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
Options
45°
95°
135°
90°
Solution
In the given problem, bisectors of the acute angles of a right angled triangle meet at O. We need to find ∠AOC.
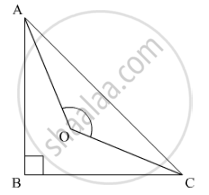
Now, using the angle sum property of a triangle
In ΔABC
∠A + ∠B + ∠C = 180°
90° + ∠A+ ∠C = 180°
∠A + ∠C = 90° ..............(1)
Now, further multiplying each of the term by 1/2in (1)
`1/2 ∠A + 1/2 ∠C = 1/2 90°`
∠OAC + ∠ACO = 45°
Also, applying angle sum property of a triangle
In ΔAOC
∠OAC + ∠ACO + ∠AOC = 180°
45° + ∠AOC = 180°
∠AOC = 180° - 45°
= 135°
Thus, ∠AOC = 135°
APPEARS IN
RELATED QUESTIONS
Show that the angles of an equilateral triangle are 60° each.
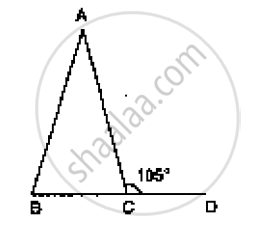
In Figure 10.24, AB = AC and ∠ACD =105°, find ∠BAC.
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, calculate the angles of the triangle.
Fill the blank in the following so that the following statement is true.
In a ΔABC if ∠A = ∠C , then AB = ......
Fill in the blank to make the following statement true.
The sum of any two sides of a triangle is .... than the third side.
In the given figure, the sides BC, CA and AB of a Δ ABC have been produced to D, E and F respectively. If ∠ACD = 105° and ∠EAF = 45°, find all the angles of the Δ ABC.
In the given figure, what is y in terms of x?

In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
If ∆PQR ≅ ∆EDF, then is it true to say that PR = EF? Give reason for your answer
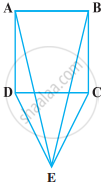
CDE is an equilateral triangle formed on a side CD of a square ABCD (Figure). Show that ∆ADE ≅ ∆BCE.