Advertisements
Advertisements
प्रश्न
If the bisectors of the acute angles of a right triangle meet at O, then the angle at Obetween the two bisectors is
विकल्प
45°
95°
135°
90°
उत्तर
In the given problem, bisectors of the acute angles of a right angled triangle meet at O. We need to find ∠AOC.
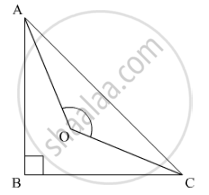
Now, using the angle sum property of a triangle
In ΔABC
∠A + ∠B + ∠C = 180°
90° + ∠A+ ∠C = 180°
∠A + ∠C = 90° ..............(1)
Now, further multiplying each of the term by 1/2in (1)
`1/2 ∠A + 1/2 ∠C = 1/2 90°`
∠OAC + ∠ACO = 45°
Also, applying angle sum property of a triangle
In ΔAOC
∠OAC + ∠ACO + ∠AOC = 180°
45° + ∠AOC = 180°
∠AOC = 180° - 45°
= 135°
Thus, ∠AOC = 135°
APPEARS IN
संबंधित प्रश्न
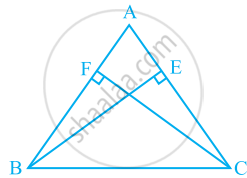
ABC is an isosceles triangle in which altitudes BE and CF are drawn to equal sides AC and AB respectively (see the given figure). Show that these altitudes are equal.
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
ABC is a triangle in which ∠B = 2 ∠C. D is a point on BC such that AD bisects ∠BAC and AB = CD.
Prove that ∠BAC = 72°.
Which of the following statements are true (T) and which are false (F):
The two altitudes corresponding to two equal sides of a triangle need not be equal.
In ΔABC, side AB is produced to D so that BD = BC. If ∠B = 60° and ∠A = 70°, prove that: (i) AD > CD (ii) AD > AC
O is any point in the interior of ΔABC. Prove that
(i) AB + AC > OB + OC
(ii) AB + BC + CA > OA + QB + OC
(iii) OA + OB + OC >` 1/2`(AB + BC + CA)
ABC is a triangle. The bisector of the exterior angle at B and the bisector of ∠C intersect each other at D. Prove that ∠D = \[\frac{1}{2}\] ∠A.
In the given figure, x + y =

In the given figure, what is y in terms of x?

In ∆ABC, BC = AB and ∠B = 80°. Then ∠A is equal to ______.
