Advertisements
Advertisements
प्रश्न
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
विकल्प
- \[90^\circ + \frac{x^\circ }{2}\]
\[90^\circ - \frac{x^\circ }{2}\]
\[180^\circ + \frac{x^\circ }{2}\]
\[180^\circ - \frac{x^\circ }{2}\]
उत्तर
In the given figure, bisects of exterior angles ∠Band ∠C meet at O and ∠A = x°
We need to find ext. ∠BOC
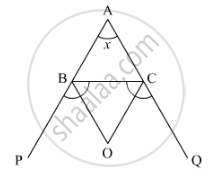
Now, according to the theorem, “if the sides AB and AC of a ΔABC are produced to P and Qrespectively and the bisectors of ∠PBC and ∠QCB intersect at O, therefore, we get,
`∠BOC = 90^\circ - 1/2 ∠A`
Hence, in ΔABC
`∠BOC = 90^\circ - 1/2 ∠A`
`∠BOC = 90^\circ - 1/2 x`
Thus,
`∠BOC = 90^\circ - x/2`
APPEARS IN
संबंधित प्रश्न
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
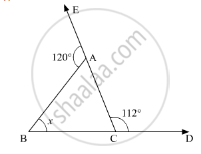
Compute the value of x in the following figure:
Fill in the blank to make the following statement true:
A triangles cannot have more than ......obtuse angles.
In the given figure, AB divides ∠DAC in the ratio 1 : 3 and AB = DB. Determine the value of x.
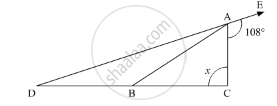
In the given figure, show that: ∠a = ∠b + ∠c
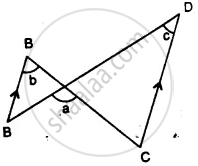
(i) If ∠b = 60° and ∠c = 50° ; find ∠a.
(ii) If ∠a = 100° and ∠b = 55° : find ∠c.
(iii) If ∠a = 108° and ∠c = 48° ; find ∠b.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
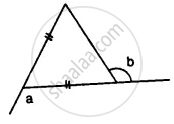
In the given figure, express a in terms of b.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
9 cm, 6 cm, 16 cm
In figure, ∠BAC = 90° and AD ⊥ BC. The number of right triangles in the figure is ______.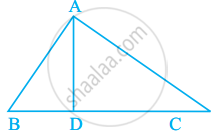
Identify three triangles in the figure.