Advertisements
Advertisements
Question
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
Options
- \[90^\circ + \frac{x^\circ }{2}\]
\[90^\circ - \frac{x^\circ }{2}\]
\[180^\circ + \frac{x^\circ }{2}\]
\[180^\circ - \frac{x^\circ }{2}\]
Solution
In the given figure, bisects of exterior angles ∠Band ∠C meet at O and ∠A = x°
We need to find ext. ∠BOC
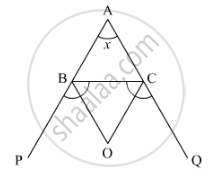
Now, according to the theorem, “if the sides AB and AC of a ΔABC are produced to P and Qrespectively and the bisectors of ∠PBC and ∠QCB intersect at O, therefore, we get,
`∠BOC = 90^\circ - 1/2 ∠A`
Hence, in ΔABC
`∠BOC = 90^\circ - 1/2 ∠A`
`∠BOC = 90^\circ - 1/2 x`
Thus,
`∠BOC = 90^\circ - x/2`
APPEARS IN
RELATED QUESTIONS
If each angle of a triangle is less than the sum of the other two, show that the triangle is acute angled.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is always ......... than either of the interior opposite angles.
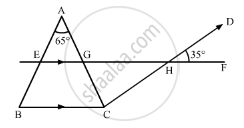
In the given figure, if AB || CD, EF || BC, ∠BAC = 65° and ∠DHF = 35°, find ∠AGH.
State, if the triangle is possible with the following angles :
40°, 130°, and 20°
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
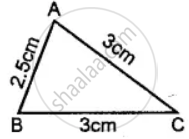
Classify the following triangle according to sides:
The length of the sides of the triangle is given. Say what types of triangles they are 3 cm, 4 cm, 5 cm.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
7 cm, 24 cm, 25 cm
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
12 cm, 12 cm, 16 cm
Can we have two acute angles whose sum is a straight angle? Why or why not?
