Advertisements
Advertisements
प्रश्न
The bisects of exterior angle at B and C of ΔABC meet at O. If ∠A = x°, then ∠BOC =
पर्याय
- \[90^\circ + \frac{x^\circ }{2}\]
\[90^\circ - \frac{x^\circ }{2}\]
\[180^\circ + \frac{x^\circ }{2}\]
\[180^\circ - \frac{x^\circ }{2}\]
उत्तर
In the given figure, bisects of exterior angles ∠Band ∠C meet at O and ∠A = x°
We need to find ext. ∠BOC
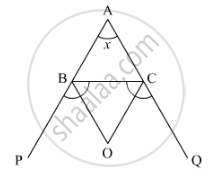
Now, according to the theorem, “if the sides AB and AC of a ΔABC are produced to P and Qrespectively and the bisectors of ∠PBC and ∠QCB intersect at O, therefore, we get,
`∠BOC = 90^\circ - 1/2 ∠A`
Hence, in ΔABC
`∠BOC = 90^\circ - 1/2 ∠A`
`∠BOC = 90^\circ - 1/2 x`
Thus,
`∠BOC = 90^\circ - x/2`
APPEARS IN
संबंधित प्रश्न
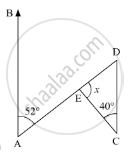
Compute the value of x in the following figure:
Is the following statement true and false :
A triangle can have two obtuse angles.
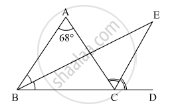
In the given figure, side BC of ΔABC is produced to point D such that bisectors of ∠ABC and ∠ACD meet at a point E. If ∠BAC = 68°, find ∠BEC.
In ΔABC, ∠B = ∠C and ray AX bisects the exterior angle ∠DAC. If ∠DAX = 70°, then ∠ACB =
Find the value of the angle in the given figure:

One angle of a triangle is 61° and the other two angles are in the ratio `1 1/2: 1 1/3`. Find these angles.
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
The angles of the triangle are 3x – 40, x + 20 and 2x – 10 then the value of x is
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
Which two triangles have ∠B in common?