Advertisements
Advertisements
प्रश्न
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
उत्तर
Given: O is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle.
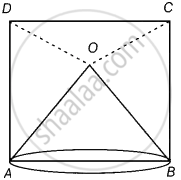
Construction: Join OC and OD.
To show: ΔOCD is an isosceles triangle.
Proof: Since, AOB is an equilateral triangle.
∴ ∠OAB = ∠OBA = 60° ...(i)
Also, ∠DAB = ∠CBA = 90° ...(ii) [Each angle of a square is 90°] [∵ ABCD is a square]
On subtracting equation (i) from equation (ii), we get
∠DAB – ∠OAB = ∠CBA – ∠OBA = 90° – 60°
i.e. ∠DAO = ∠CBO = 30°
In ΔAOD and ΔBOC,
AO = BO ...[Given] [All the side of an equilateral triangle are equal]
∠DAO = ∠CBO ...[Proved above]
And AD = BC ...[Sides of a square are equal]
∴ ΔAOD ≅ ΔBOC ...[By SAS congruence rule]
Hence, OD = OC ...[By CPCT]
In ΔCOD,
OC = OD
Hence, ΔCOD is an isosceles triangle.
Hence proved.
APPEARS IN
संबंधित प्रश्न
Compute the value of x in the following figure:
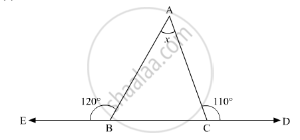
Compute the value of x in the following figure:
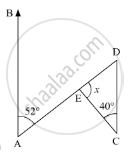
In the given figure, AB || DE. Find ∠ACD.

Is the following statement true and false :
Sum of the three angles of a triangle is 180 .
Is the following statement true and false :
All the angles of a triangle can be equal to 60°.
Is the following statement true and false :
An exterior angle of a triangle is equal to the sum of the two interior opposite angles.
Calculate the angles of a triangle if they are in the ratio 4: 5: 6.
Can you draw a triangle with 25°, 65° and 80° as angles?
In figure, points lying in the interior of the triangle PQR are ______, that in the exterior are ______ and that on the triangle itself are ______.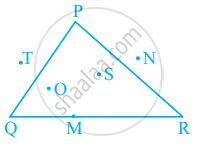
Can we have two acute angles whose sum is an acute angle? Why or why not?
