Advertisements
Advertisements
Question
O is a point in the interior of a square ABCD such that OAB is an equilateral triangle. Show that ∆OCD is an isosceles triangle.
Solution
Given: O is a point in the interior of a square ABCD such that ΔOAB is an equilateral triangle.
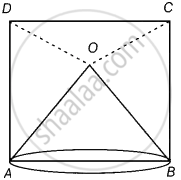
Construction: Join OC and OD.
To show: ΔOCD is an isosceles triangle.
Proof: Since, AOB is an equilateral triangle.
∴ ∠OAB = ∠OBA = 60° ...(i)
Also, ∠DAB = ∠CBA = 90° ...(ii) [Each angle of a square is 90°] [∵ ABCD is a square]
On subtracting equation (i) from equation (ii), we get
∠DAB – ∠OAB = ∠CBA – ∠OBA = 90° – 60°
i.e. ∠DAO = ∠CBO = 30°
In ΔAOD and ΔBOC,
AO = BO ...[Given] [All the side of an equilateral triangle are equal]
∠DAO = ∠CBO ...[Proved above]
And AD = BC ...[Sides of a square are equal]
∴ ΔAOD ≅ ΔBOC ...[By SAS congruence rule]
Hence, OD = OC ...[By CPCT]
In ΔCOD,
OC = OD
Hence, ΔCOD is an isosceles triangle.
Hence proved.
APPEARS IN
RELATED QUESTIONS
Can a triangle have All angles more than 60°? Justify your answer in case.
Fill in the blank to make the following statement true:
An exterior angle of a triangle is always ......... than either of the interior opposite angles.
If two sides of a triangle are 5 cm and 1.5 cm, the length of its third side cannot be ______.
In a triangle ABC, ∠A = 45° and ∠B = 75°, find ∠C.
One angle of a triangle is 60°. The other two angles are in the ratio of 5: 7. Find the two angles.
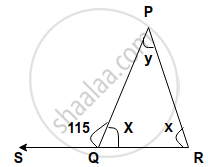
Find, giving a reason, the unknown marked angles, in a triangle drawn below:
The length of the three segments is given for constructing a triangle. Say whether a triangle with these sides can be drawn. Give the reason for your answer.
17 cm, 7 cm, 8 cm
In a ∆ABC, AB = AC. The value of x is ________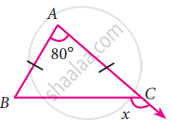
If an angle of a triangle is equal to the sum of the other two angles, find the type of the triangle
Can we have two acute angles whose sum is an obtuse angle? Why or why not?
