Advertisements
Advertisements
Question
ABC is a right triangle with AB = AC. Bisector of ∠A meets BC at D. Prove that BC = 2AD.
Solution
We have given, ΔABC which is an isosceles right triangle with AB = AC and AD is the bisector of ∠A.
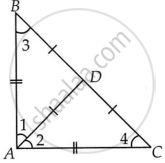
Now in ΔABC,
AB = AC ...[Given]
⇒ ∠C = ∠B ...(1) [Angles opposite to equal sides are equal]
Now, in ΔABC, ∠A = 90°
∠A + ∠B + ∠C = 180° ...[Angle sum property of Δ]
⇒ 90° + ∠B + ∠B = 180° ...[From (1)]
⇒ 2∠B = 90°
⇒ ∠B = 45°
⇒ ∠B = ∠C = 45° or ∠3 = ∠4 = 45°
Also, ∠1 = ∠2 = 45° ...[∵ AD is bisector of ∠A]
Also, ∠1 = ∠3, ∠2 = ∠4 = 45°
⇒ BD = AD, DC = AD ...(2) [Sides opposite to equal angles are equal]
Thus, BC = BD + DC = AD + AD ...[From (2)]
⇒ BC = 2AD
APPEARS IN
RELATED QUESTIONS
Which of the following statements are true (T) and which are false (F):
If any two sides of a right triangle are respectively equal to two sides of other right triangle, then the two triangles are congruent.
In two triangles ABC and DEF, it is given that ∠A = ∠D, ∠B = ∠E and ∠C =∠F. Are the two triangles necessarily congruent?
If the following pair of the triangle is congruent? state the condition of congruency :
In Δ ABC and Δ DEF, AB = DE, BC = EF and ∠ B = ∠ E.
Use the information in the given figure to prove:
- AB = FE
- BD = CF

If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔQRP, AB = QR, ∠B = ∠R and ∠C = P.
In a triangle ABC, D is mid-point of BC; AD is produced up to E so that DE = AD.
Prove that :
(i) ΔABD and ΔECD are congruent.
(ii) AB = CE.
(iii) AB is parallel to EC
If AP bisects angle BAC and M is any point on AP, prove that the perpendiculars drawn from M to AB and AC are equal.
In the given figure, AB = DB and Ac = DC.
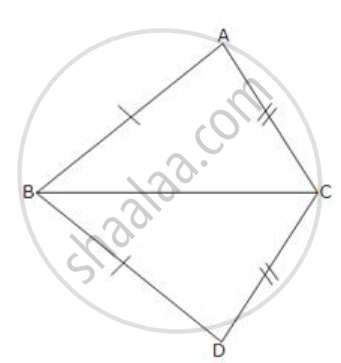
If ∠ ABD = 58o,
∠ DBC = (2x - 4)o,
∠ ACB = y + 15o and
∠ DCB = 63o ; find the values of x and y.
In the following figure, AB = AC and AD is perpendicular to BC. BE bisects angle B and EF is perpendicular to AB.
Prove that : ED = EF

In the parallelogram ABCD, the angles A and C are obtuse. Points X and Y are taken on the diagonal BD such that the angles XAD and YCB are right angles.
Prove that: XA = YC.
