Advertisements
Advertisements
Question
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
Solution
Given: ABCD is a quadrilateral in which AB = BC and AD = CD.
To show: BD bisects both the angles ABC and ADC.
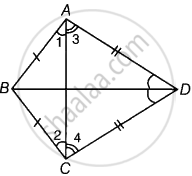
Proof: Since, AB = BC ...(Given)
∴ ∠2 = ∠1 ...(i) [Angles opposite to equal sides are equal]
And AD = CD ...[Given]
⇒ ∠4 = ∠3 ...(ii) [Angles opposite to equal sides are equal]
On adding equations (i) and (ii), we get
∠2 + ∠4 = ∠1 + ∠3
⇒ ∠BCD = ∠BAD ...(iii)
In ΔBAD and ΔBCD,
AB = BC ...[Given]
∠BAD = ∠BCD ...[From equation (iii)]
And AD = CD ...[Given]
∴ ΔBAD ≅ ΔBCD ...[By SAS congruence rule]
Hence, ∠ABD = ∠CBD and ∠ADB = ∠CDB i.e., BD bisects the angles ABC and ADC. ...[By CPCT]
APPEARS IN
RELATED QUESTIONS
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(EF)`
Find the measure of each angle of an equilateral triangle.
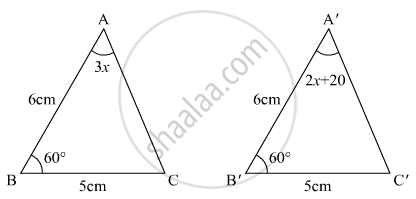
In the given figure, the measure of ∠B'A'C' is
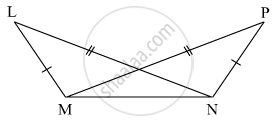
As shown in the following figure, in ΔLMN and ΔPNM, LM = PN, LN = PM. Write the test which assures the congruence of the two triangles. Write their remaining congruent parts.
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the following figure, OA = OC and AB = BC.

Prove that: AD = CD
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
If the perpendicular bisector of the sides of a triangle PQR meet at I, then prove that the line joining from P, Q, R to I are equal.
In the figure, AP and BQ are perpendiculars to the line segment AB and AP = BQ. Prove that O is the mid-point of the line segments AB and PQ.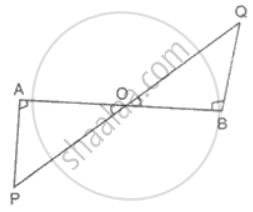
In ΔABC, AB = AC, BM and Cn are perpendiculars on AC and AB respectively. Prove that BM = CN.
