Advertisements
Advertisements
Question
In the given figure, the measure of ∠B'A'C' is
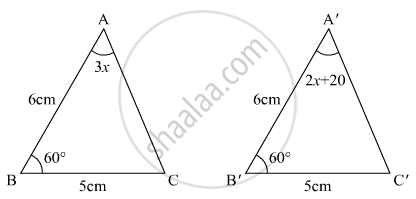
Options
50°
60°
70°
80°
Solution
We have to find B’A’C’

ince triangles are congruent
So ∠A = ∠A
3X = 2X + 20
X = 20
Now in A’B’C’
∠A + ∠B + C = 180° (By property of triangle)
60° + 60° + ∠C = 180°
∠C = 60°
∠A = 2X + 20
`= 2 xx 20° + 20°`
= 40° + 20
= 60°
Hence (b) B’A’C’ = 60°.
APPEARS IN
RELATED QUESTIONS
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
State, whether the pairs of triangles given in the following figures are congruent or not:

In a circle with center O. If OM is perpendicular to PQ, prove that PM = QM.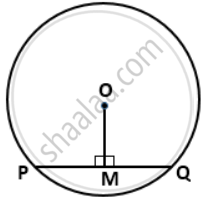
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.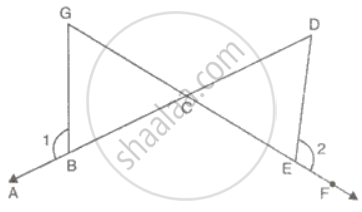
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
In triangles ABC and DEF, AB = FD and ∠A = ∠D. The two triangles will be congruent by SAS axiom if ______.
“If two sides and an angle of one triangle are equal to two sides and an angle of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆YZX ≅ ∆PQR
