Advertisements
Advertisements
प्रश्न
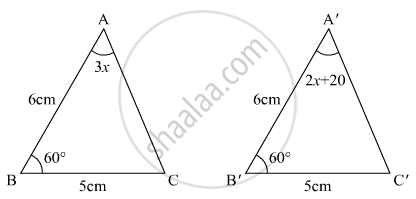
In the given figure, the measure of ∠B'A'C' is
पर्याय
50°
60°
70°
80°
उत्तर
We have to find B’A’C’

ince triangles are congruent
So ∠A = ∠A
3X = 2X + 20
X = 20
Now in A’B’C’
∠A + ∠B + C = 180° (By property of triangle)
60° + 60° + ∠C = 180°
∠C = 60°
∠A = 2X + 20
`= 2 xx 20° + 20°`
= 40° + 20
= 60°
Hence (b) B’A’C’ = 60°.
APPEARS IN
संबंधित प्रश्न
BD and CE are bisectors of ∠B and ∠C of an isosceles ΔABC with AB = AC. Prove that BD = CE.
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In ΔABC and ΔPQR and, AB = PQ, BC = QR and CB and RQ are extended to X and Y respectively and ∠ABX = ∠PQY. = Prove that ΔABC ≅ ΔPQR.
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.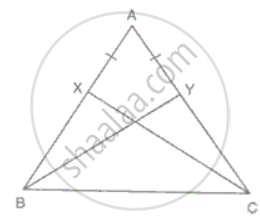
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
Two figures are congruent, if they have the same shape.
