Advertisements
Advertisements
प्रश्न
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
उत्तर
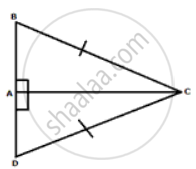
In ΔABC and ΔADC
∠BAC = ∠DAC ...(90°)
BC = DC
AC = AC ...(common)
Therefore, ΔABC ≅ ΔADC ...(SSA criteria)
Hence, ∠BCA = ∠DCA
Thus, AC bisects ∠BCD.
APPEARS IN
संबंधित प्रश्न
In a ΔPQR, if PQ = QR and L, M and N are the mid-points of the sides PQ, QR and RP
respectively. Prove that: LN = MN.
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
In the following figure, OA = OC and AB = BC.

Prove that: AD = CD
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

State, whether the pairs of triangles given in the following figures are congruent or not:

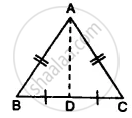
Prove that:
- ∆ ABD ≅ ∆ ACD
- ∠B = ∠C
- ∠ADB = ∠ADC
- ∠ADB = 90°
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.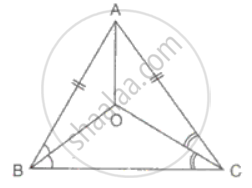
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.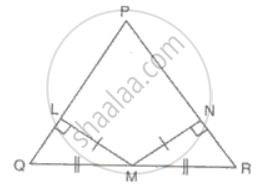
ΔABC is an isosceles triangle with AB = AC. GB and HC ARE perpendiculars drawn on BC.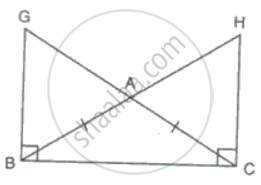
Prove that
(i) BG = CH
(ii) AG = AH
The top and bottom faces of a kaleidoscope are congruent.
