Advertisements
Advertisements
प्रश्न
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.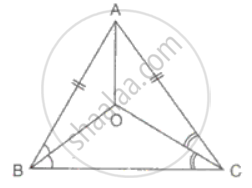
उत्तर
In ΔABC,
Since AB = AC
∠C = ∠B ...(angles opposite to the equal sides are equal)
BO and CO are angle bisectors of ∠B and ∠C respectively
Hence, ∠ABO = ∠OBC = ∠BCO = ∠ACO
Join AO to meet BC at D
In ΔABO and ΔACO and
AO = AO
AB = AC
∠C = ∠B =
Therefore, ΔBAO ≅ ΔACO ...(SAS criteria)
Hence, ∠BAO = ∠CAO
⇒ AO bisects angle BAC
In ΔABO and ΔACO
and AB = AC
AO = AO
∠BAD = ∠CAD = ...(proved)
ΔBAO ≅ ΔACO ...(SAS criteria)
Therefore,
BO = CO.
APPEARS IN
संबंधित प्रश्न
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
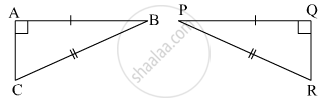
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
In the given figure, seg AB ≅ seg CB and seg AD ≅ seg CD. Prove that ΔABD ≅ ΔCBD.

In ΔTPQ, ∠T = 65°, ∠P = 95° which of the following is a true statement?
If the following pair of the triangle is congruent? state the condition of congruency :
In ΔABC and ΔDEF, ∠B = ∠E = 90o; AC = DF and BC = EF.
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(BC = 5cm,AC = 6cm,∠C = 80°);
ΔXYZ;(XZ = 6cm,XY = 5cm,∠X = 70°).
In a triangle ABC, if D is midpoint of BC; AD is produced upto E such as DE = AD, then prove that:
a. DABD andDECD are congruent.
b. AB = EC
c. AB is parallel to EC
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.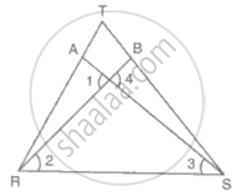
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
