Advertisements
Advertisements
प्रश्न
In the figure, RT = TS, ∠1 = 2∠2 and ∠4 = 2∠3. Prove that ΔRBT ≅ ΔSAT.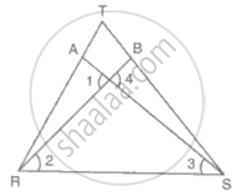
उत्तर
∠1 = 2∠2 and ∠4 = 2∠3
1 = 22 and 4 = 23∠1 = ∠4 ...(vertically opposite angles)
⇒ 2∠2 = 2∠3 or ∠2 = ∠3 ........(i)
∠R = ∠S = ...(since RT = TS and angle opposite to equal sides are equal)
⇒ ∠TRB = ∠TSA = .........(ii)
In ΔRBT and ΔSAT.
RT = TS
∠TRB = ∠TSA
∠RTB = ∠STA = ...(common)
Therefore, ΔRBT ≅ ΔSAT. ...(ASA criteria)
APPEARS IN
संबंधित प्रश्न
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to ∠E
If ΔDEF ≅ ΔBCA, write the part(s) of ΔBCA that correspond to `bar(DF)`
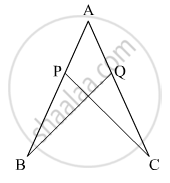
In the given figure, if AB = AC and ∠B = ∠C. Prove that BQ = CP.
Which of the following is not a criterion for congruence of triangles?
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
If the following pair of the triangle is congruent? state the condition of congruency:
In ΔABC and ΔPQR, BC = QR, ∠A = 90°, ∠C = ∠R = 40° and ∠Q = 50°.
On the sides AB and AC of triangle ABC, equilateral triangle ABD and ACE are drawn. Prove that:
- ∠CAD = ∠BAE
- CD = BE
In the following diagram, ABCD is a square and APB is an equilateral triangle.
(i) Prove that: ΔAPD≅ ΔBPC
(ii) Find the angles of ΔDPC.
Two right-angled triangles ABC and ADC have the same base AC. If BC = DC, prove that AC bisects ∠BCD.
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
