Advertisements
Advertisements
प्रश्न
PQRS is a quadrilateral and T and U are points on PS and RS respectively such that PQ = RQ, ∠PQT = ∠RQU and ∠TQS = ∠UQS. Prove that QT = QU.
उत्तर
∠PQT = ∠RQU .....(i)
∠TQS = ∠UQS .....(ii)
Adding (i) and (ii)
∠PQS = ∠RQS
In ΔPQS and ΔRQS
∠PQS = ∠RQS
PQ = RQ ...(given)
QS = QS ...(common)
Therefore, ΔPQS ≅ ΔRQS ...(SAS criteria)
Hence, ∠QPS = ∠QRS
Now in ΔPQT and ΔRQU
∠QPS = ∠QRS
PQ = RQ ...(given)
∠PQT = ∠RQU ...(given)
Therefore, ΔPQT ≅ ΔRQU ...ASA criteria)
Hence, QT =QU.
APPEARS IN
संबंधित प्रश्न
If ΔABC ≅ ΔFED under the correspondence ABC ↔ FED, write all the Corresponding congruent parts of the triangles.
In ΔPQR ≅ ΔEFD then ED =
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.

In the following diagram, AP and BQ are equal and parallel to each other.

Prove that:
(i) ΔAOP≅ ΔBOQ.
(ii) AB and PQ bisect each other.
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
A is any point in the angle PQR such that the perpendiculars drawn from A on PQ and QR are equal. Prove that ∠AQP = ∠AQR.
In the given figure, AB = DB and AC = DC. Find the values of x and y.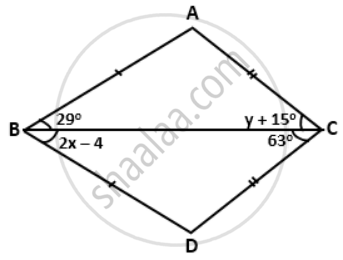
ABCD is a quadrilateral in which AB = BC and AD = CD. Show that BD bisects both the angles ABC and ADC.
