Advertisements
Advertisements
प्रश्न
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
उत्तर
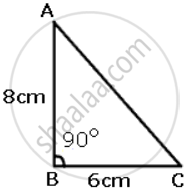
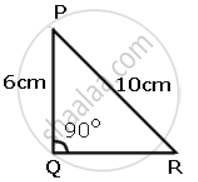
In ΔABC and ΔPQR
∠B = ∠Q
BC = PQ
By Pythagoras theorem,
PR2 = PQ2 + QR2
102 = 62 + QR2
100 = 36 + QR2
QR = `sqrt(100 - 36)`
QR = `sqrt(64)` = 8cm
AB = QR
Therefore,
ΔABC ≅ ΔPQR ...(SAS criteria).
APPEARS IN
संबंधित प्रश्न
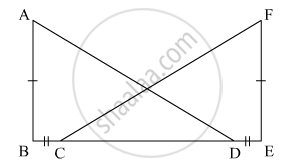
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
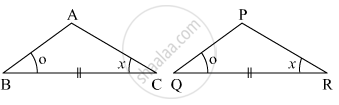
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
From the information shown in the figure,
In ΔABC and ΔPQR
∠ABC ≅ ∠PQR
seg BC ≅ seg QR
∠ACB ≅ ∠PRQ
∴ ΔABC ≅ ΔPQR ...`square` test
∴ ∠BAC ≅ `square` ...corresponding angles of congruent triangles.
`{:("seg AB" ≅ square),("and" square ≅ "seg PR"):}}` ...corresponding sides of congruent triangles
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
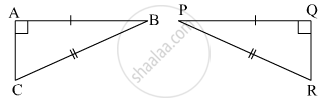
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.
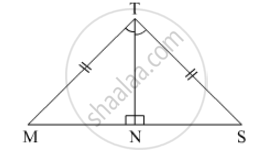
State, whether the pairs of triangles given in the following figures are congruent or not:
Δ ABC in which AB = 2 cm, BC = 3.5 cm and ∠C = 80° and Δ DEF in which DE = 2 cm, DF = 3.5 cm and ∠D = 80°.
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(AB = 8cm,BC = 6cm,∠B = 100°);
ΔPQR;(PQ = 8cm,RP = 5cm,∠Q = 100°).
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.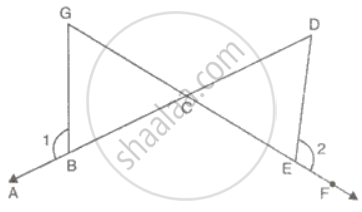
“If two angles and a side of one triangle are equal to two angles and a side of another triangle, then the two triangles must be congruent.” Is the statement true? Why?
The congruent figures super impose each other completely.
Without drawing the triangles write all six pairs of equal measures in the following pairs of congruent triangles.
∆XYZ ≅ ∆MLN
