Advertisements
Advertisements
प्रश्न
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.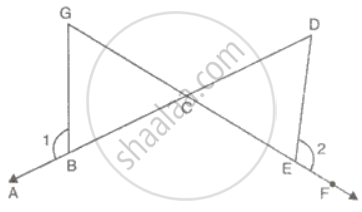
उत्तर
In ΔGCB and ΔDCE and
∠1 + ∠GBC = ∠2 + ∠DEC = 180°
∠1 = ∠2 =
⇒ ∠GBC = ∠DEC
BC = CE
∠GCB = ∠DCE = ...(vertically opposite angles)
Therefore,
ΔGCB ≅ ΔDCE ....(ASA criteria).
APPEARS IN
संबंधित प्रश्न
CDE is an equilateral triangle formed on a side CD of a square ABCD. Show that ΔADE ≅ΔBCE.
If ΔPQR≅ ΔEFD, then ∠E =
In the given figure, AB ⊥ BE and FE ⊥ BE. If BC = DE and AB = EF, then ΔABD is congruent to
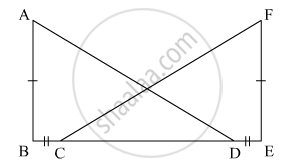
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the following figure, OA = OC and AB = BC.
Prove that:
(i) ∠AOB = 90o
(ii) ΔAOD ≅ ΔCOD
(iii) AD = CD
State, whether the pairs of triangles given in the following figures are congruent or not:

AD and BE are altitudes of an isosceles triangle ABC with AC = BC. Prove that AE = BD.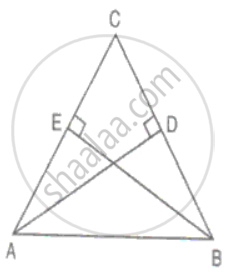
In the given figure ABCD is a parallelogram, AB is Produced to L and E is a midpoint of BC. Show that:
a. DDCE ≅ DLDE
b. AB = BL
c. DC = `"AL"/(2)`
Prove that in an isosceles triangle the altitude from the vertex will bisect the base.
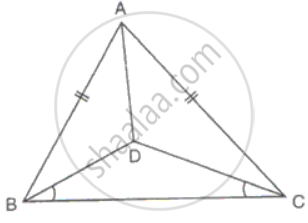
In ΔABC, AB = AC. D is a point in the interior of the triangle such that ∠DBC = ∠DCB. Prove that AD bisects ∠BAC of ΔABC.