Advertisements
Advertisements
प्रश्न
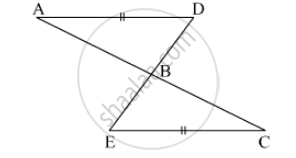
In the figure, BC = CE and ∠1 = ∠2. Prove that ΔGCB ≅ ΔDCE.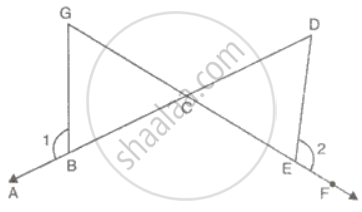
उत्तर
In ΔGCB and ΔDCE and
∠1 + ∠GBC = ∠2 + ∠DEC = 180°
∠1 = ∠2 =
⇒ ∠GBC = ∠DEC
BC = CE
∠GCB = ∠DCE = ...(vertically opposite angles)
Therefore,
ΔGCB ≅ ΔDCE ....(ASA criteria).
APPEARS IN
संबंधित प्रश्न
In a squared sheet, draw two triangles of equal areas such that
The triangles are congruent.
What can you say about their perimeters?
In a ΔABC, if AB = AC and ∠B = 70°, find ∠A.
In two right triangles one side an acute angle of one are equal to the corresponding side and angle of the othe Prove that the triangles are congruent.
If ΔPQR≅ ΔEFD, then ∠E =
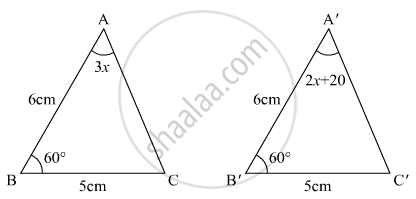
In the given figure, the measure of ∠B'A'C' is
If ABC and DEF are two triangles such that ΔABC \[\cong\] ΔFDE and AB = 5cm, ∠B = 40°
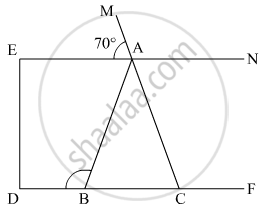
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
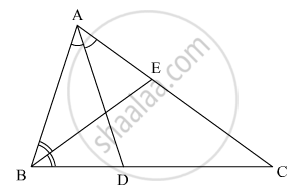
In the given figure, ABC is a triangle in which ∠B = 2∠C. D is a point on side BC such that ADbisects ∠BAC and AB = CD. BE is the bisector of ∠B. The measure of ∠BAC is
In the adjacent figure, seg AD ≌ seg EC Which additional information is needed to show that ∆ ABD and ∆ EBC will be congruent by A-A-S test?
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

