Advertisements
Advertisements
प्रश्न
In ΔABC, AB = AC and the bisectors of angles B and C intersect at point O.Prove that BO = CO and the ray AO is the bisector of angle BAC.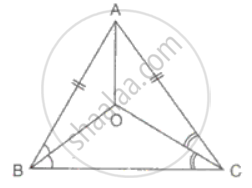
उत्तर
In ΔABC,
Since AB = AC
∠C = ∠B ...(angles opposite to the equal sides are equal)
BO and CO are angle bisectors of ∠B and ∠C respectively
Hence, ∠ABO = ∠OBC = ∠BCO = ∠ACO
Join AO to meet BC at D
In ΔABO and ΔACO and
AO = AO
AB = AC
∠C = ∠B =
Therefore, ΔBAO ≅ ΔACO ...(SAS criteria)
Hence, ∠BAO = ∠CAO
⇒ AO bisects angle BAC
In ΔABO and ΔACO
and AB = AC
AO = AO
∠BAD = ∠CAD = ...(proved)
ΔBAO ≅ ΔACO ...(SAS criteria)
Therefore,
BO = CO.
APPEARS IN
संबंधित प्रश्न
Prove that the sum of three altitudes of a triangle is less than the sum of its sides.
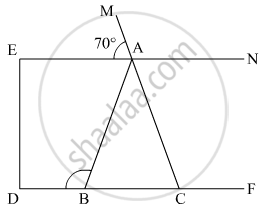
In the given figure, if AE || DC and AB = AC, the value of ∠ABD is
In the following example, a pair of triangles is shown. Equal parts of triangle in each pair are marked with the same sign. Observe the figure and state the test by which the triangle in each pair are congruent.

By ______ test
ΔXYZ ≅ ΔLMN
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
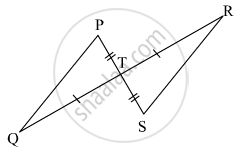
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
The following figure has shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: (i) BN = CM (ii) ΔBMC≅ΔCNB

Prove that:
(i) ∆ ABC ≅ ∆ ADC
(ii) ∠B = ∠D
Which of the following pairs of triangles are congruent? Give reasons
ΔABC;(∠B = 90°,BC = 6cm,AB = 8cm);
ΔPQR;(∠Q = 90°,PQ = 6cm,PR = 10cm).
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.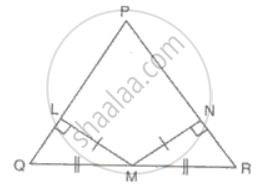
In ΔABC, X and Y are two points on AB and AC such that AX = AY. If AB = AC, prove that CX = BY.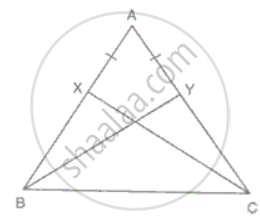
In the figure, AC = AE, AB = AD and ∠BAD = ∠EAC. Prove that BC = DE.
