Advertisements
Advertisements
प्रश्न
In ΔPQR, LM = MN, QM = MR and ML and MN are perpendiculars on PQ and PR respectively. Prove that PQ = PR.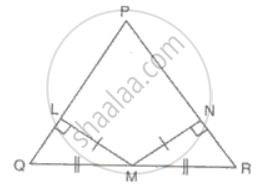
उत्तर
In ΔQLM and ΔRNM
QM = MR
LM = MN
∠QLM = ∠RNM = 90°
Therefore, ΔQLM ≅ ΔRNM ...(RHS criteria)
Hence, QL = RN ..........(i)
Join PM
In ΔPLM and ΔPNM and
PM = PM ...(common)
LM = MN
∠PLM = ∠PNM = 90°
Therefore, ΔPLM ≅ ΔPNM ...(RHS criteria)
Hence, PL = PN ..........(ii)
From (i) and (ii)
PQ = PR.
APPEARS IN
संबंधित प्रश्न
ΔPQR and ΔABC is not congruent to ΔRPQ, then which of the following is not true:
In a ΔABC, if AB = AC and BC is produced to D such that ∠ACD = 100°, then ∠A =
In an isosceles triangle, if the vertex angle is twice the sum of the base angles, then the measure of vertex angle of the triangle is
Observe the information shown in pair of triangle given below. State the test by which the two triangles are congruent. Write the remaining congruent parts of the triangles.
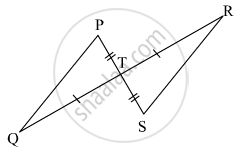
From the information shown in the figure,
in ΔPTQ and ΔSTR
seg PT ≅ seg ST
∠PTQ ≅ ∠STR ...[Vertically opposite angles]
∴ ΔPTQ ≅ ΔSTR ...`square` test
∴ `{:("∠TPQ" ≅ square),("and" square ≅ "∠TRS"):}}` ...corresponding angles of congruent triangles
seg PQ ≅ `square` ...corresponding sides of congruent triangles
From the information shown in the figure, state the test assuring the congruence of ΔABC and ΔPQR. Write the remaining congruent parts of the triangles.
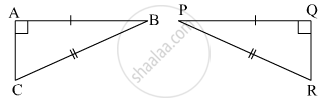
In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

In the pair of triangles in the following figure, parts bearing identical marks are congruent. State the test and the correspondence of vertices by the triangle in pairs is congruent.

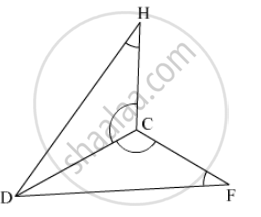
In the pair of triangles given below, the parts shown by identical marks are congruent. State the test and the one-to-one correspondence of vertices by which the triangles in the pair are congruent, the remaining congruent parts.
The following figure shown a triangle ABC in which AB = AC. M is a point on AB and N is a point on AC such that BM = CN.
Prove that: ΔAMC≅ ΔANB

